niedziela, 19 czerwca 2022
Kaleidoscope of prime numbers
”Mathematics is the music of mind "
James Joseph Sylvester
PREFACE
The "Kaleidoscope of Prime Numbers" presents primes in a new light, in the light of their essential properties. What are these basic properties of prime numbers, we will see on the example of numbers from 1 to 9, where there are as many as four, which are, how they arise and in what order they follow each other.
I further explain how the prime numbers are woven into the sequence of natural numbers, revealing all their so far hidden beauty, which is a reflection of the centuries-old order of beauty and truth encoded in them.
PROPERTIES OF NUMBERS FROM 1-9
We only have these nine numbers, and with them we can write down all the numbers. So the properties they have are shared by all numbers. If all the numbers between 1 and 9 are written in ascending order 1, 2, 3, 4, 5, 6, 7, 8, 9, and added to the numbers in descending order, we will see the same 9, 8, 7, 6, 5 , 4, 3, 2, 1, complete the top ten.
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 45
(9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1) = 45
10 + 10+10 + 10+10 + 10+10 + 10+10 = 90
This basic law of complement to a given ten applies to all numbers and only complements each other as shown in the table below.
For the number 20 we have 8 prime numbers (2,3,5,7,11,13,17,19) and 2 products of the number three (9,15), which are half of the number 20/2 = 10 = 8 + 2 From 20 to 100, i.e. in 80 numbers, we have 17 primes (23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97) and 23 their products (21.25.27.33.35.39.45.49.51.55.57.63.65.69.75.77.81.85.87.91.93.95.99) which complete each other to the half of 80/2 = 40 = 17 + 23. And for a total of 25 primes to 100 we have 25 complementary products 100/2 = 50 = (8 + 17) + (2 + 23) = 25 + 25, or 25 primes plus 9 products of numbers greater than three 25 + 9 = 34, is padded by 2 + 14 = 16 products of three for half of the given quantity 100/2 = 50 = 34 + 16.
There is one more property associated with adding the digits from 1 to 9, when added one to the other, they create successive triangular numbers 1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15, 15 + 6 = 21 , 21 + 7 = 28, 28 + 8 = 36 36 + 9 = 45, and if we now divide every second of them by 1, 2, 3, 4, we get the next odd numbers 3/1 = 3, 10/2 = 5, 21/3 = 7, 36/4 = 9. The sum of two consecutive triangular numbers is always a square number 1 + 3 = 4, 2², 3 + 6 = 9, 3², 6 + 10 = 16, 4², 10 + 15 = 25, 5², 15 + 21 = 36, 6², 21 + 28 = 49, 7², 28 + 36 = 64, 8², 36 + 45 = 81, 9².
It is clear from this how a sequence of natural numbers is an extremely ordered sequence of numbers.
If we write all the numbers from 1 to 9 in ascending and descending order, we will get the sequence 17 = 9 + 8 numbers, the sum of which is 81 and to this we add 17 digits written in descending and increasing order, we will see how they themselves complement 10, and their sums up to 81 + 89 = 170. This shows how the prime numbers are systematically spread, always by the same number 17, which, like a pantograph, allows its products to complete each other to half of each magnitude. (17 + / 23, 33, 43, ... / = 40, 50, 60)
Such decreasing and increasing sequences of natural numbers / 9-8-7-6-5-4-3-2-1-2-3-4-5-6-7-8-9 = 89 / form 17 pairs of extreme components / 1-2-3-4-5-6-7-8-9-8-7-6-5-4-3-2-1 = 81 / used as factors (9 * 1) = 9, (8 * 2) = 16, (7 * 3) = 21, (6 * 4) = 24, (5 * 5) = 25 give the products of decreasing odd numbers / 9 + 7 = 16 + 5 = 21 + 3 = 24 + 1 = 25 /, which proves that these factors, i.e. all natural numbers, create identical intermediate sums / 9 + 1 = 8 + 2 = 7 + 3 = 6 + 4 = 5 + 5 = 4 + 6 = 3 + 7 = 2 + 8 = 1 + 9 = 2 + 8 = 3 + 7 = 4 + 6 = 5 + 5 = 6 + 4 = 7 + 3 = 8 + 2 = 9 + 1 = 17 (10) = 170 /.
This parabola of numbers clearly shows the relationship between the five numbers / 1 3 5 7 9 / and the numbers on its arc / 9 + 7 = 16 + 5 = 21 + 3 = 24 + 1 = 25 /, and the Pythagorean equations 3² + 4² = 5², as well as the numbers of the equations 25 + 9 = 34 and 25 - 9 = 16 which say that the sum and difference of numbers with the same parity is an even number. These laws apply to the entire set of natural numbers. Another parabola is formed by the numbers 1 through 9, and this is the congruence parabola. Two integers a b are equivalent to or congruent with modulo p if p divides (a – b). Hence we can write a ≡ b mod (p), and this is what happens with the numbers 1 through 9. 9 - 2 = 7/7, 8 - 1 = 7/7, 7 - 0 = 7/7, 6 - 1 = 5/5, 5 - 2 = 3/3, 4 - 2 = 2/2.
Therefore, they unfold like a congruent deck of 10 cards up to the seventh card.
As nine digits are completed by 9 by increasing numbers on the diagonal, so seven digits are completed by 7 using four proper ones (7, 6, 5, 4) and four from the diagonal (3, 2, 1, 0). Then we get 7 complete sequences of numbers from 0 to 7 congruent to each other modulo 7. 7 (7), 49 - 42, 7 (6), 42 - 35, 7 (5), 35 - 28, 7 (4), 28 - 21, 7 (3), 21 - 14, 7 (2), 14 - 7, 7 (1) = 7/7.
The seven-digit number 9999997/7 = 1,428,571, is absolutely divisible by seven. I
If we add one to two, their sum creates the next adjacent natural number 3. The next square number 4 out of 5 and 6 creates the same sum as 7 and 8, i.e. 15. The next square number with three consecutive numbers creates the same sum as the next 3 numbers 9 + 10 + 11 + 12 = 13 + 14 + 15 = 42. This is because the first and last components of these identical sums always increase by the next odd number 1 -3- 4 -5- 9 -7-16, 3 -5- 8 -7- 15 -9- 24, and all others by the next even number 1-4- 5, 2 -4- 6, 3 -4- 7, 4 -6-10, 5 -6- 11, 6 -6- 12, 7 -6- 13, 8 -6-14 -8- 24, .. And the sums and spacing between the sums are always a number divisible by three 3/3 -12/3- 15/3 -27/3- 42/3 -48/3- 90/3 -75/3 - 165/3 -108/3 - 273/3 -147/3 - 420/3. All of this is contained in a little magic square of nine numbers from 1 to 9.
f we put numbers from 1 to 9 on the circle every 40⁰ and we draw lines from 1 to 4, from 4 to 2, from 2 to 8, from 8 to 5, from 5 to 7 and from 7 to 1, then we will draw two pairs adjacent to each other triangles with the lengths of their sides (4 - 1 = 3, 8 - 5 = 3, 4 - 2 = 2, 7 - 5 = 2, 8 - 2 = 6, 7 - 1 = 6)
It proves the perfect order of the whole sequence of natural numbers, which consists in 50% of even and odd numbers, i.e. prime numbers and their products. Such basic numbers are not determined by nature by the method of random tossing a coin or dice "God doesn't play dice with the world", but based on the ability to create identical intermediate sums from the extreme pairs of numbers preceding the given quantity. So it is not a random action, but a cause and effect. Chance and chaos are simply unacceptable to mathematics.
SUM OF CONSECUTIVE NUMBERS
Observe this pyramid of integers, from 1 to 63, arranged in a natural staircase of numbers in the natural order of counting.
If we add one to two, their sum creates the next adjacent natural number 3. The next square number 4 out of 5 and 6 creates the same sum as 7 and 8, i.e. 15. The next square number with three consecutive numbers creates the same sum as the next 3 numbers 9 + 10 + 11 + 12 = 13 + 14 + 15 = 42. This is because the first and last components of these identical sums always increase by the next odd number 1 -3- 4 -5- 9 -7-16, 3 -5- 8 -7- 15 -9- 24, and all others by the next even number 1-4- 5, 2 -4- 6, 3 -4- 7, 4 -6-10, 5 -6- 11, 6 -6- 12, 7 -6- 13, 8 -6-14 -8- 24, .. And the sums and spacing between the sums are always a number divisible by three 3/3 -12/3- 15/3 -27/3- 42/3 -48/3- 90/3 -75/3 - 165/3 -108/3 - 273/3 -147/3 - 420/3. All of this is contained in a little magic square of nine numbers from 1 to 9.
Since the number 5 is the arithmetic mean of the numbers 1 to 9 [(1 +2 + 3 + 4) + 5 + (6 + 7 + 8 + 9)] = 45/9 = 5 and divides this sequence into 2 parts of 4 numbers, complementing in the first part with extreme pairs up to 5 = (1 + 4) (2 + 3), and in the second part up to 15 = (6 + 9) (7 + 8), hence their sum is 2 (5) = 10 and 2 (15) = 30. Besides, all the extreme numbers complement 10 = (1 + 9) (2 + 8), therefore 4 (1 + 9) + 5 = 4 (10) + 5 = 45. That the number 5 standing in the middle of this sequence allows all extreme numbers to complete to 10 (1 + 9), (2 + 8), (3 + 7), (4 + 6) and this property is used to make the sum of 3 horizontal numbers in a magic square , vertically and diagonally, it was always 15.
The above table shows how the sum of the even numbers 2 + 4 + 6 + 8 = 20 = 1 + 3 + 7 + 9 and the odd numbers are equal to each other because the pairs of the extreme numbers complete 10 (2 + 8) (4 + 6) ( 1 + 9) (3 + 7). Hence we can wr
ite 2 (20) + 5 = 40 + 5 = 45 as the sum of the numbers 1 through 9. The prime numbers themselves can be arranged in a similar way. Please note that the numbers of their sums 177 and 276 added together 1 + 7 + 7 = 15, 2 + 7 + 6 = 15, form the same sum as in the magic square
But there is nothing magical about it, it's just the arithmetic means of those nine or sixteen numbers complete the top ten. (9 + 45 + 36 = 90) (21 + 36 + 52 + 31 = 140).
The arithmetic mean of 5 numbers is calculated by dividing their sum by 5 (1 + 2 + 3 + 4 + 5)/5 = 15/5 = 3, or simply by adding 1 to the given number and dividing it by two (n + 1)/2 = the arithmetic mean, (5 + 1)/2 = 6/2 = 3. Indeed, the number 3 divides this sequence of numbers into 2 equal parts of pairs of complementing numbers to 6 = 1 + 5 = 2 + 4, hence it is enough to quickly count them all Multiply 6 times 2 and add 3 [2 (6) + 3 = 12 + 3 = 15].
Table of arithmetic means of odd numbers from 3 to 101.
The table of the arithmetic means of odd numbers from 3 to 101, shows how the means themselves added consecutively to each other 2 + 3 = 5, 3 + 4 = 7, ... make up all the odd numbers starting at 5.
The fact that the odd numbers are 1 greater than the even numbers (2n + 1) results in the property that the even number preceding them from 1 is completed to the following odd number 8 + 1 = 9, 6 + 1 = 7, 4 + 1 = 5, 2 + 1 = 3, and the other pairs of the preceding extreme numbers 2 + 7 = 9, 3 + 6 = 9, 4 + 5 = 9, 2 + 5 = 7, 3 + 4 = 7, 2 + 3 = 5. And this is the principle on which the construction of all odd numbers, that is, prime numbers and their products, is based.
We know that any integer greater than one, divisible only by one and itself, is prime if it consists of pairs of extreme numbers preceding which whose greatest common divisor is one. 7 = (6 + 1)/1, (5 + 2)/1, (4 + 3)/1. So we can write the number 7 as three identical intermediate sums 7/1 + 7/1 + 7/1 = 21/3 = 7/1, with the common divisor of one, which proves that it is a prime number.
If the sum of the preceding numbers, i.e. a given triangular number, primes up to a given number, it means that each pair of components does not have a common divisor greater than one and the given number is prime. Factoring a given triangular number into prime factors less than a given number means that at least one pair of terms has a common divisor greater than one and the given number is composite. 9 = (8 + 1)/1 = (7 + 2)/1 = (6 + 3)/3 = (5 + 4)/1, 4(9) = 36/2 = 18/2 = 9/3 = 3/3 = 1, (2*2)(3* 3) = 36, so the number 9 is a composite number. The number 11 is prime because the five pairs of identical sums that make it up, added outwardly as the numbers preceding the given number, do not have a common divisor greater than 1, and they add up to 55, a triangular number completely divisible by the number of identical intermediate sums equal to half the number in front of it. an even number. (10 + 1)/1, = (9 + 2)/1, = (8 + 3)/1, = (7 + 4)/1, = (6 + 5)/1, 5(11) = 55/5 = 11.
Triangular numbers 3, 10, 21, 36, 55, ... as a sum of numbers preceding a given odd number, consist of n - the number of pairs of terms from opposite ends of the list of preceding numbers, equal to half of the preceding even number 2/2, 4 / 2, 6/2, 8/2, 10/2, which, if they do not have a common divisor greater than 1, form identical intermediate sums of only prime numbers (4 + 1)/1, (2 + 3)/1, 5 + 5 = 10/2 = 5, and if they have at least one common divisor greater than 1, they form identical intermediate sums only of complex numbers (8 + 1)/1, (7 + 2)/1, (6 + 3)/3, (5 + 4)/1, 9 + 9 + 9 + 9 = 36/4 = 4 * 9 = (2 * 2) (3 * 3).
This systematic process of determining which number is the product of prime or prime, as we can see in the table below, is a good example of an algorithm for testing this:
[(n - 1) (n)] /
But not all odd numbers are prime numbers, and although they are formed on the same principle, when decoding them we will see that they not only consist of the outermost pairs of relatively prime numbers that precede them, but also numbers whose highest common divisor is a number greater than one. Then we deal with complex numbers (9/3, 15/5, 21/7, 25/5, 27/3, 33/11, 35/7, 39/13, 45/5, 49/7, 51/17), because 9 = (4 + 5)/1, but also 9 = (3 + 6)/3, 51 = (25 + 26)/1, but also 51 = (17 + 34)/17.
According to additive number theory, each odd number can be represented as the sum of two different components of the extreme preceding numbers, making up identical intermediate sums, having no common divisor greater than one and then it is prime, e.g. 7 = (6 + 1)/1 = (5 + 2)/1 = (4 +3) /1, or having a common divisor greater than 1 and then complex, e.g. 9 = (8 + 1)/1 = (7 + 2)/1 = (6 +3) /3 = (5 + 4)/1. We can see that such distributions that make up identical intermediate sums are always as many as half the preceding even number, so 6/2 = 3 to 7, 8/2 = 4 to 9, 10/2 = 5 to 10. In this way we can easily calculate the sum of all the preceding numbers by multiplying the identical sums equal to the given number by half the preceding even number, e.g. 3(7) = 21, 4(9) = 36, 5(11) = 55. Factoring these numbers into prime factors is irrefutable proof that the given number consists of all prime numbers 21/3 = 7, 3(7) = 21, 55/5 = 11, 5(11) = 55, or complex 36/3 = 12/3 =
4/2 = 2, 3(3) = 9, 2(2) = 4, 4(9) = 36. Realizing that adding pairs of words from opposite ends of a list of numbers preceding an odd number always yields identical subtotals (6 + 5) = 11 = (7 + 4), tells us whether the given triangular number, as the sum of the numbers preceding the given quantity, consists of only prime numbers (55/5 = 11) or complex numbers (36/4 = 9).
If the sum of the preceding numbers, i.e. a given triangular number, primes up to a given number, it means that each pair of components does not have a common divisor greater than one and the given number is prime. Factoring a given triangular number into prime factors less than a given number means that at least one pair of terms has a common divisor greater than one and the given number is composite. 9 = (8 + 1)/1 = (7 + 2)/1 = (6 + 3)/3 = (5 + 4)/1, 4(9) = 36/2 = 18/2 = 9/3 = 3/3 = 1, (2*2)(3* 3) = 36, so the number 9 is a composite number. The number 11 is prime because the five pairs of identical sums that make it up, added outwardly as the numbers preceding the given number, do not have a common divisor greater than 1, and they add up to 55, a triangular number completely divisible by the number of identical intermediate sums equal to half the number in front of it. an even number. (10 + 1)/1, = (9 + 2)/1, = (8 + 3)/1, = (7 + 4)/1, = (6 + 5)/1, 5(11) = 55/5 = 11.
Triangular numbers 3, 10, 21, 36, 55, ... as a sum of numbers preceding a given odd number, consist of n - the number of pairs of terms from oppo
site ends of the list of preceding numbers, equal to half of the preceding even number 2/2, 4 / 2, 6/2, 8/2, 10/2, which, if they do not have a common divisor greater than 1, form identical intermediate sums of only prime numbers (4 + 1)/1, (2 + 3)/1, 5 + 5 = 10/2 = 5, and if they have at least one common divisor greater than 1, they form identical intermediate sums only of complex numbers (8 + 1)/1, (7 + 2)/1, (6 + 3)/3, (5 + 4)/1, 9 + 9 + 9 + 9 = 36/4 = 4 * 9 = (2 * 2) (3 * 3).
This systematic process of determining which number is the product of prime or prime, as we can see in the table below, is a good example of an algorithm for testing this:
[(n – 1)(n)]/2 = n/2 = t | p = (n = p) lub (n)/2 = t | p = (p < n) = p(p’).
It is based on the fundamental property of prime numbers to form n - the number of pairs of components with identical intermediate sums that do not have a common divisor greater than 1. Then the triangular number as the sum of all the preceding numbers decomposes into prime factors up to the given number, which means that is prime. When it decomposes into prime factors less than a given number, it is a composite number. An algorithm is a method by which we can solve a problem by following its instructions. When we apply this, then we have an irrefutable certificate confirming that the given number is a prime number or the product of prime numbers.
Let's check the properties of the number (1,378,565,437 - 1) / 2, from which we subtract 1 and divide by 2, to see how many pairs of components with identical intermediate sums are formed, which is equal to 1,378,565,436 / 2 = 689,282,718 pairs and by this number we multiply it to get the sum of all preceding numbers, i.e. a triangular number t = 950,221,331,356,217,766, which decomposes into prime factors up to a given number, i.e. a given number is prime, because it consists of 689,282,718 pairs of components of identical intermediate sums of prime 1,378,565,437.
1,378,565,437(689,282,718) = 950,221,331,356,217,766 (1 + 1,378,565,436)/1 = 1,378,565,437 950,221,331,356,217,766/3 = 316,740,443,785,405,922 (2 + 1,378,565,435)/1 = 1,378,565,437 316,740,443,785,405,922/2 = 158,370,221,892,702,961 (3 + 1,378,565,434)/1 = 1,378,565,437 158,370,221,892,702,961/114,880,453 = 1,378,565,437 (4 + 1,378,565,433)/1 = 1,378,565,437 114,880,453*6 = 689,282,718 (689,282,718 + 689,282,719)/1 = 1,378,565,437
Note that the sum of the four primes is 17 = 2 + 3 + 5 + 7, and this number is half of 34/2 = 17 indicates that the primes form 17 pairs with nine products greater than three padded by 16 products. the numbers three to half the size.
π(x) + ∑[p(p’)] = ½N, 25 + (9 + 16) = 100/2, 5² + (3² + 4²) = 10²/2, 25 + 9 = 34/2 = 17
COLLECTION OF NATURAL NUMBERS
In the table composed of numbers in a natural order (1, 2, 3, 4, 5, 6, 7, 8, 9, 10,) we can see that prime numbers and their products are subject to strict rules here: The sum and difference of two numbers with the same same parity, is an even number (9 + 25 = 34, 25 - 9 = 16), and a different odd number (4 + 1 = 5, 4 - 1 = 3), and that from 59, which is a prime number 17, they will come by 17 (34, 51, 68, 85, 102, 119, 136) in proportion to the number of their products, which, if it is of the same parity as the number of prime numbers, completes the prime numbers in the even interval to half of the given quantity ( 34 + 38 = 72), when in an odd range up to half of a given quantity (51 + 66 = 117) according to the equation π(x) + ∑[p(p')] = ½N - half of a given quantity is the sum the number of prime numbers and their products that occur up to a given quantity. And just as the hypotenuse in a triangle depends on the side legs, half of the size depends on an even or odd multiple of 17/34, 51, 68, 85, 102 / supplemented by an even or odd number of products of primes /38, 66, 103, 136,177/ to even or odd half of a given size (72, 117, 171, 221, 279).
From now on the number of prime numbers will always increase naturally by the next multiple of 17 (17-17-34-17-51-17-68-17-85-17-102), when at 85 = 5(17) the number of products of prime numbers reaches the value of 136 = 8 (17), which gives a total of 221 = 13(17) primes and their products in 442 numbers. So 85 prime numbers + 136 their products = 221, are half the sequence of 442 numbers among which they appear in the strictly defined ratio 5 + 8 = 13, 5 : 8 : 13.
And the prime numbers and their products are evenly distributed as they follow each other in 20 columns every 40-80 numbers and in rows with a constant number of places for primes and their products greater than 3, supplemented to ½N by the products of the number 3 (4 - 3 - 3)(6 - 7 - 7), i.e. 6 places in this line, 4 may be occupied by prime numbers, and 2 by their products greater than 3, similarly in lines for 7 places, 5 for prime numbers and 2 for their products greater than 3. Only the first row has space for 8 prime numbers, and since every third number in each row is the product of 3, there will be 2 places for the products of number 3. In the next row among 6 places, there are 4 places for the products of number 3, and among the 7 places there are 3 places for the products of the number three.
It is the complementary arrangement of prime numbers together with products greater than 3 and products of 3 (8 + 2 = 6 + 4 = 7 + 3 = 7 + 3 = 6 + 4 = 34 + 16 = 50) that makes these numbers develop pantographically to half of the given quantity 334 + 166 = 500.
If the sequence of primes follows strict rules such as the strict ratio of prime numbers to its products, which in the decimal system takes strictly defined values according to the rule 17, 34, 51, 68 primes are complemented by their products to the full ten e.g . 17 + (23, 33, 43, 63, 73, 83, 93), 34 + (86, 96, 106, 116, 126, 136, 146, 156, 166, 176), 51 + (119, 139, 169, 179 , 199, 209, 229), 68 + (202, 222, 232, 272, 312), depending on the space in which the quantities are distributed. However, the rule that the sum of the prime numbers and their products is always equal to half of the given quantity to which they occur is always kept. π (x) + ∑ [p (p ')] = ½N, 68 + 102 = 170, (2: 3: 5). And this is proof that the prime numbers are not arranged haphazardly, but systematically according to strict rules.
RATIO OF PRIMARY NUMBERS TO THEIR PRODUCTS
In fact, the distribution of prime numbers depends on a strict relation to their products, and this is due to the ability to create intermediate sums identical to a given quantity. Up to 10 we have 4 prime numbers (2 + 3 + 5 + 7) = 17, they form 4 identical intermediate sums up to 10 [2 + 8 = 10, 3 + 7 = 10, 5 + 5 = 10, 7 + 3 = 10, (8 + 7 + 5 + 3) = 23, 17 + 23 = 40/4 = 10]. According to this scheme, the ratio of prime numbers to their products will be shaped, that is, for 40 odd numbers in a given interval, there may be 17 primes and 23 of their products.
This is what it looks like in the line chart. Here the sum of 4 primes (2 + 3 + 5 + 7 = 17), padded with the sum of differences up to 10 (8 + 7 + 5 + 3 = 23), shows the ratio of 17 primes / from 20 - 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 to 100 / up to 23 of their products / 21, 25, 27, 33, 35, 39, 45 , 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95, 99 / in 17 + 23 = 40 numbers as half of the given quantity. (100 - 20 = 80/2 = 40)
π(x) + Σ[p(p')] = ½N.
As you can see in the 10-column table below, there are 4 pairs in the first row, i.e. 8 prime numbers (2, 3) (5, 7) (11, 13) (17, 19), and only 2 products of 3 (9 and 15 ), (8 + 2 = 10). In the following rows, this ratio is as follows (4 + 6) = (5 + 5) = (5 + 5) = (3 + 7) = (4 + 5 + 5 + 3) = 17 + 8 = 25, prime numbers to (6 + 5 + 5 + 7) = 23 + 2 = 25 their products, so in the fifth row this ratio becomes even, and in the sixth row there are 5 prime numbers and their products equal to 30, i.e. prime numbers to their products are in the ratio 1: 1.
Up to N 20 we have 8 prime numbers / π (20) = 8 / and only 2 products of the number 3/9, 15 /, and in the next N 80 there will be 17 prime numbers, so that at N 100 - π (100) equals 8 + 17 = 25, supplemented to the whole ten by 23 products of the numbers 3, 5, 7 (21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77 , 81, 85, 87, 91, 93, 95, 99) / 17 + 23 = 40 /, which is half of the 80 numbers among which they are and align the number of products with the number of prime numbers 2 + 23 = 25, 25 + 25 = 50 to half the size.
In the following rows 6 to 11, the ratio is 17/33, i.e. in the range of 50 numbers (50 = 17 + 33), there are 17 primes and 33 of their products, i.e. prime numbers are placed among their products in a strictly defined ratio . However, the rule is always kept that the sum of the prime numbers and their products is equal to half of the given quantity /π(x) + Σ[p(p')] = ½N, 68 + 102 = 170, 2: 3: 5/.
In the following rows / 34 - 46 / the ratio of prime numbers to their products is doubled from 17/43 to 34/86 because it covers the range 34 + 86 = 120 numbers. We also have a range of 17 + 43 = 60 numbers, 17 + 53 = 70 numbers, 34 + 66 = 100 numbers, 34 + 96 = 130 numbers, and 34 + 106 = 140 numbers.
We cannot say that prime numbers always occur every 20 numbers, but it is certain that they come in strict relation to their products in groups of, 17 + (23, 33, 43, 53, 63, 73, 83, 93) of numbers , 34 + (66, 86, 96, 106, 116, 126, 136, 146, 156, 166, 176) numbers, 51 + (119, 139, 169, 179, 199, 229), 68 + 202 = 270 numbers, 68 + 222 = 290 numbers, 68 + 232 = 300 numbers, 68 + 272 = 340 numbers, as we can see in the table below to 10960 numbers.
It is difficult to imagine a more even distribution of prime numbers and their products than those resulting from the way they follow one another at constant distances, every 20 numbers, /3 - 23 - 43 - 63 - 83 - 103, 131 - 151 - 171 - 191 - 211 - 231 - 251 - 271 - 291/, complementing each other in a strictly defined ratio (17/23, 17/33, 17/43, ..) to half of a given quantity /½N/. Then they form 16 columns, i.e. 4 times 4 for each characteristic number of units / 1 - 3 - 7 - 9/16 and 17 numbers each and 2 times two, i.e. 4 columns for the products of the number 5 by 16 + 17 = 33(2 ) = 66. How easy it is to calculate a total of 13 columns of 17 numbers each is /13(17) = 221/ plus 1 = 222 and 7 columns of 16 numbers 7(16) = 112 + 222 gives 334 numbers. In this there are only primes /7(10) + 6(11) + 2 (12) + 8 = 168 /, and products of numbers greater than 3 is /4(7) + 9(6) + 66 + 9 + 5 + 4 = 166/.
The equal distance / 20 / from each other in a zigzag pattern in the table below / 9, 29, 49, 69, 89, 109 / results in a place for 8 prime numbers and 2 products of the number 3. / 8 in the first row of 20 columns. + 2 = 10 / In the following rows there will be space for 6 primes and their products greater than 3, and 4 products of the number 3/6 + 4 = 10 /, then for 7 primes and their products greater than 3, and 3 products of the number 3/7 + 3 = 10 / and again for 7 prime numbers and their products greater than 3, and 3 products of the number 3/7 + 3 = 10 / and further for 6 primes and their products greater than 3, and 4 products numbers 3/6 + 4 = 10 /. Adding 8 + 6 + 7 + 7 + 6 = 34 we get 34 places which are occupied by prime numbers and their products greater than 3, and 2 + 4 + 3 + 3 + 4 = 16, the number of places which are taken by products of number 3. 34 + 16 = 50, so up to 100 we have 34 primes and their products greater than 3, and 16 products of 3. 34/16/50 is the basic ratio of the products of 3 to prime numbers and their products greater than 3, which will repeat every 50 numbers until infinity. Here, up to 1000, we see 10/16 + 16 + 17 + 17 + 16 + 17 + 17 + 16 + 17 + 17/ = 4(16) + 6(17) = 64 + 102 = 166 products of the number 3, and 10 /34 + 34 + 33 + 33 + 34 + 33 + 33 + 34 + 33 + 33/ = 4(34) + 6(33) = 136 + 198 = 334 prime numbers and their products greater than 3. Of this constant ratio of products the number 3 to the remaining numbers shows that they have a direct impact on the number of primes up to a given magnitude /34 = 9 + 25 - 9 = 16/. It is the constant number of products of the number 3 in a given row 16 = 3 + 3 + 4 + 3 + 3 and 17 = 4 + 3 + 3 + 4 + 3 that makes them complemented by a constant number (34) of prime numbers and their greater products than 3 in the next five rows 34 = 7 + 7 + 6 + 7 + 7.
This basic ratio of the products of 3 (16/34) to primes and their products greater than 3 is reflected in the strict ratio of primes to their products. As in the row of 6 or 7 prime numbers and their products greater than 3, there could not be products of 3, more than 4 or 3, /7 + 7 + 7 + 7 + 6 = 34, 3 + 3 + 3 + 3 + 4 = 16/, /5(10) = 50 = 34 + 16/, as a complement to the half of a given quantity (20/2 = 10), so here for 8 prime numbers there are 2 products of 3, /9, 15/ , for 4 prime numbers there are 6 products, for 5 primes there are 5 primes for them, for 3 primes there are 7 products, which in total 8 + (4 + 5 + 5 + 3) = 8 + 17 = 25 numbers the first supplemented by 2 + (6 + 5 + 5 + 7) = 2 + 23 = 25 of their products to 25 + 25 = 50 half of the given quantity.
PRIMARY NUMBER FUNCTION π (x)
Until now, the prime numbers have seemed to be quite randomly distributed among other numbers. However, the number of primes is constantly smaller for the further areas we consider, and their number is decreasing both to half the number of numbers in a given quantity and their products 25:25:50 1/1/2, 68: 102: 170, 2/3/5, 85: 136: 221, 5/8/13. When it comes to their arrangement, prime numbers are subject to one rule that the sum of prime numbers and their products make up half of a given quantity / π (x) + ∑ [p (p ')] = ½N /, i.e. they are mutually dependent. Interestingly, the number of quantities of their products / ∑ p (p ') / is a number with the same parity as the number of prime numbers π (x). (25 + 25 = 50, 168 + 332 = 500, 1229 + 3771 = 5000, 9592 + 40408 = 50000, 78498 + 421502 = 500000, ....)
The sum and difference of two numbers with the same parity is always even, and therefore divisible by two. The rule of half the sum and the difference of primes and their products allows us to calculate the number of primes up to half of a given quantity, because this half consists of half the sum and the difference of numbers with the same parity.
Theorem: If the number of quantities of their products /∑p(p')/, is of the same parity as the number of quantities of primes π (x), then half of their sum and difference added when their products are more than prime numbers, or subtracted when there are fewer primes than their products it gives the exact value of π(x) to half of the given quantity.
Proof:
If up to 100 we have 25 primes and 9 products of numbers greater than 3, then half of the sum and the difference are added when the products of numbers greater than 3 are less than primes (25 + 9) / 2 + (25 - 9) / 2 = 17 + 8 = 25, or subtracted when there are more than primes (2105 + 1229) / 2 - (2105 - 1229) / 2 = 1667 - 438 = 1229, gives the exact value of π (x) for the given quantity. So we can write a formula.
[∑p(p’)> 3 - ∑(p)]/2 ± [∑p(p’)> 3 + ∑ (p)]/2 = π(x)
The 168-number sequence of primes from 2 - 997, is completed by 166 products of 3 (9 - 999), and 166 products of numbers greater than 3 [168 + (166 + 166)] = 168 + 332 = 500, halfway given size. From this layout it is clear that the products of the number 3, which increases as half of a given quantity in a predictable geometric progression 16, [166 = 16(10) + 6, 1666 = 166 (10) + 6], affect the number of prime numbers and their products greater than 3. That is, according to the basic ratio, there are 34 = 25 prime numbers plus 9 of their products greater than 3. /16 + 34 = 50 = 25 + (16 + 6 +3)/
The more of these products of number 3/16, 166, 1666 /, the less space remains for primes in this natural sequence of numbers, always arithmetically expanding by the perfect number 6 (3 - 9 - 15 - 21 - 27) (5 - 11 - 17 - 23 - 29) (7 - 13 - 19 - 25 - 31).
PERFECT ORDER
How evenly distributed the prime numbers are shown by these 3 columns of even numbers from 0 - 96, from 2 - 98, from 4 - 100, and three columns of odd numbers from 1 - 97, from 3 - 99, from 5 - 101, 17 numbers in each hence the multiples of 17, 34/2, 51/3, 68/4, 85/5, 102/6 form the diagonal of this rectangle of numbers. Therefore, the sum of the numbers in each column is divisible by (816/17 = 48) indicating which number is the arithmetic mean of the 17 numbers in that column. (48, 49, 50, 51, 52, 53) 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 = 153/17 = 9, i.e. nine is the arithmetic mean of 17 numbers, that is divides this sequence of 17 numbers into two parts of eight numbers each 8+/1/+8 = 17. The number 17 performs the same function in six sequential sequences of numbers from 0 - 96, where the arithmetic mean of the sequence is 816/17 = 48, from 1 - 97, where the arithmetic mean of the sequence is 833/17 = 49, from 2 - 98, where the arithmetic mean of the sequence is 850/17 = 50, from 3 - 99, where the arithmetic mean of the sequence is 867/17 = 51, from 4 - 100, where the arithmetic mean of the sequence is 884/17 = 52, from 5 - 101, where the arithmetic mean of the sequence is 901/17 = 53. Adding the second and sixth sum of odd numbers 833 + 901 = 1734/17 we see, that the number 17 falls in it 102 times because it is the sum of their arithmetic means 833/17 + 901/17 = 49 + 53 = 102. The arrangement of prime numbers and their products greater than 3, in the order of one hundred and two, is the most perfect possible, because the ratio of the sum of the numerical values of the primes and their products greater than 3 (833 + 901 = 1734/17 = 102), to the sum of the numerical values products of the number 3 (867/17 = 51) is always constant and equals 1734/867 = 2. Also the ratio of the arithmetic mean of sequences of prime numbers and their products greater than 3 to the arithmetic mean of the products of 3 is constant and equals 102/51 = 2.
In the table above, we see 25 prime numbers with 9 of their products greater than 3 (25, 35, 49, 55, 65, 77, 85, 91, 95), written in 2 columns of 17 numbers in the form of a sequence with a constant interval 6. It is the number 17 = 25 + 9 = 34/2 that makes the primes and products so evenly distributed in the first sequence 12 primes plus 5 products is 17 and in the second sequence 13 primes plus 4 products is 17, so you can write a new sequence 9 - (8) - 17 - (8) - 25, which says that 25 primes and 9 products greater than 3 are contained in two 17-segment sequences. It also shows how many products greater than 3 are fewer (17 - 9 = 8) and there are more primes (25 - 17 = 8) distributed over 2 sequences, because 17 + 8 = 25 and 17 - 8 = 9.
This leads to a balanced distribution of prime numbers and their products greater than 3 included in the geometric sequence 3 (q) in the numbers 4 - 30 - 34 - 300 - 334 - 3000 - 3334. (34 = 9 + 25, 334 = 166 + 168, 3 334 = 2 105 + 1 229), that is ∑ (p) + [p (p ')]> 3 = ∑ [p (p')]> 3 + π (x) always supplemented to ½ N by the products of the number 3 (16, 166, 1 666), as a sum of two constant numbers 34 + 16 = 50, 334 + 166 = 500, 3 334 + 1 666 = 5,000, and ta the sum grows in the geometric sequence of 5 (q). This makes the half of the sum of the prime numbers and their products greater than 3, (25 + 9) / 2 = 34/2 = 17 one number subtracted or added from half the difference between them (25 - 9 = 16/2 = 8) , you can equate these two numbers 9 + 8 = 17 = 25 - 8, 168 - 166 = 2/2 = 1, 166 + 1 = 167 = 168 - 1, 2105 - 1229 = 876/2 = 438, 2105 - 438 = 1667 = 1229 + 438 to half the sum of prime numbers and their products greater than 3.
So there is a close relationship between the number of arriving primes π (x) and their products greater than three /∑[p(p')]> 3/, which increase exponentially 3(q), as shown in the table below. /3(q) = ∑[p(p')]> 3 + π(x) 30 = 9 + 21, 300 = 157 + 143, ../ That is, if there are 4 prime numbers in the top ten, then to 100 there cannot be more than 3(10) = 30, i.e. 21 primes plus 9 of their products greater than 3, which is equal to 30. 4 + 30 = 34 + 300 = 334 + 3000 = 3334,. ..
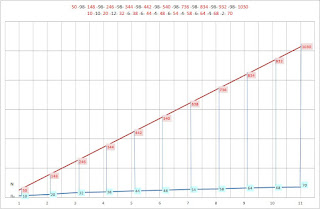
Thus, the puzzle of the distribution of prime numbers has been solved. Henceforth the sequence of primes is not similar to a random sequence of numbers, but to an exponentially ordered 3 (q) increasing sequence of primes and their products greater than 3, complemented with the products of 3 to half of the given quantity. So the sum of prime numbers and their products greater than three π(x) + ∑p(p')> 3 equals the difference between a half of a given quantity and the products of three ½N - i(3), 25 + 9 = 34 = 50 - 16 and grows exponentially 3(q), 34 - 300 - 334 - 3000 - 3334. The ratio of the prime numbers to their products is therefore determined by the complement to the half of the given quantity / π (x) + ∑ p (p ') = ½N and is 17 + (23, 33, 43, 53, 63, 73, 83, 93) each, 34 + each (66, 86, 96, 106, 116, 126, 136, 146, 156, 166, 176), 51 + (119, 139, 169, 179, 199, 229) each, 68 + (102, 202, 222, 232, 272) / numbers each, with additional proportions forming within these ratios, e.g. 68(p) + 102 ∑p(p') = 170 (½N), 2: 3: 5, 180 (p) + 360 ∑ p (p') = 540 (½N), 1: 2: 3. Then such sequences on the plot radar look like this.
It looks better when in 25 columns we have 10 numbers each [(25)10 = 250], and in 24 columns we have 11 numbers each [24(11) = 264] which in total means 514 = 1028/2 prime numbers and their products being a half of given size regularly spaced at zigzag intervals 48 to the left (11-59) and 50 to the right (59-109) for a total of 48 + 50 = 98 (59-157). The numbers arranged in this way make up 8
left-handed product sequences of three (9-57, 15-63, 21-69, 27-75, 33-81, 39-87, 45-93, 51-99) 5 right-handed product sequences of five (55-155. 65-115, 25-125, 35-85, 95-145), and 7 columns of the products of the number seven (49-343, 203-301, 161-259, 119-217, 77-371, 133-329, 91- 287).
This symmetrical arrangement resembles a full sunflower. The prime numbers of which are the same as the products of numbers greater than 3, i.e. 172, form 16 left-handed and 25 right-handed sequences, with the twins being only left-handed.
In this line graph, we can see how 515, half of the 1030 numbers, is right in the center, which shows the ideal distribution of all 514 = 172 (p) + 172 [p (p ')> 3] + 170 [3 (p)] numbers. On the other hand, the radar chart gives the numbers a galactic arrangement of left-hand and right-handed spirals.
Primes and tins positioned both at zigzag intervals 48 to the left (11 - 59) and 50 to the right (59 - 109), and in increments of 48 + 50 = 98 (59 - 157), and 50 to the left (11- 61) and 52 to the right (61-113) as well as in the progress of 50 + 52 = 102 (11-113) they spread as evenly as possible.
We can see it in these two charts where both the primes and the tins increase in almost equal amounts. There can be from 13 to 19 primes in 98 numbers padded by products up to half of this quantity, 13 + 36 = 49 = 19 + 30, and twins from 2 to 12.
There is clearly a jump in increments of every 10 twins. There are 38 to the number of 344, and two units further 2(98) = 196 there are 38 + 6 = 44 + 4 = 48 6 + 4 = 10 more, similarly from 48 + 6 = 54 + 4 = 58 + 6 = 64 + 4 = 68.
The same is observed when the space is only 48 numbers. In 48 numbers there can be 5 to 10 primes padded by products up to half of this quantity 14 + 10 = 24 = 5 + 19, and twins from 2 to 6.
There is clearly a jump in increments of every 10 twins. Up to 338 there are 38, and four units further 4 (48) = 192 there are 38 + 2 = 40 + 4 = 44 + 2 = 46 + 2 = 48, 2 + 4 + 2 + 2 = 10 more, similarly from 48 + 2 = 50 + 4 = 54 + 4 = 58 + 2 = 60 + 6 = 66 + 2 = 68.
Thus, from the apparent disorder of prime numbers emerges the extraordinary beauty of the ratio of prime numbers to their products, which always complement each other to a half of a given quantity. In this way, I have just proved that prime numbers are not only ordered according to the laws of arithmetic, but also that their systematic occurrence is not random and chaotic, but completely automatic and ordered according to their basic properties, since they are subject to the immutable laws of arithmetic that determine their number to a given size with an accuracy of one!
All this generates the most wonderful harmony and admirable beauty and truth, so that after the Book of Wisdom 11:20 we can exclaim:
"But you have precisely defined everything in terms of measure, number and weight."
The apparent disorder is regulated, for which thanks be to God, for the order on 102, which consists of 17 double right-handed sequences every n (102) - 419 - 521 - 421 - 523 and 40 left-handed sequences of homonymous primes every n (100) - 7 - 107 - 307 - 607 and 10 product sequences of 5 (25 – 125 – 325 – 425).
The line chart shows with what accuracy pairs of primes and their products greater than 3 pantographically always expand by 102 numbers to the right (5 - 107, 7 - 109) and 96 numbers to the left (5 - 101, 7 - 103). This is why among 34 numbers to 100 there are 25 primes and 9 their products greater than 3 (25 + 9 = 34/2 = 17, 25 = 8 + 17 - 8 = 9), and there are 168 prime numbers up to 1000. and 166 products of numbers greater than 3 (168 + 166 = 334/2 = 167, 168 = 1 + 167 - 1 = 166).
Q E D
"DEO GRATIAS - LET GOD THANKS WILL BE! ”
TABLES OF FIRST NUMBERS FROM 2 – 13577
Subskrybuj:
Komentarze do posta (Atom)

































































Brak komentarzy:
Prześlij komentarz